Photo reference: https://computersciencewiki.org/index.php/Binary_tree
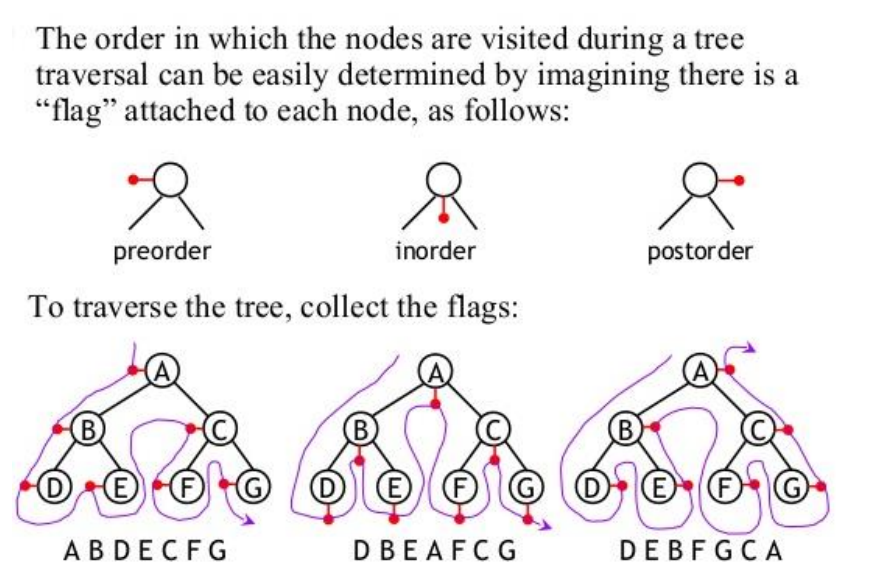
This neat little trick above saved me a lot of pain and is much quicker to get the traversals. Just think preorder = left, inorder = center, postorder = right. Then weave the string from the top left, to the bottom, to the center, and around until you get to the top right. Wherever the string would 'hook' into a line, write down that number as the next one in that type of traversal.
Given a binary tree, return the inorder traversal of its nodes' values.
Every recursive problem can be done iteratively using a stack. Recursive calls are simply utilizing the call stack that is an inherent part of the programming language. Don't forget to take into account the space the stack/recursive calls take up when doing the O notation for space!
Recursive solution:
public IListTime: O(n)InorderTraversal(TreeNode root) { List result = new List (); Helper(root, result); return result; } public void Helper(TreeNode root, List result) { if (root == null) return; Helper(root.left, result); result.Add(root.val); Helper(root.right, result); }
Space: O(log n) on average. O(n) worst case if tree is one giant linked list going in one direction.
Iterative solution using a stack:
public IListTime: O(n)InorderTraversal(TreeNode root) { List result = new List (); Stack stack = new Stack (); TreeNode curr = root; while(curr != null || stack.Count != 0) { while(curr != null) { stack.Push(curr); curr = curr.left; } curr = stack.Pop(); result.Add(curr.val); curr = curr.right; } return result; }
Space: O(n)



